The Heads Hypothesis: A Unifying Statistical Approach Towards Understanding Multi-Headed Attention in BERT
Madhura Pande || 03 Sep 2021
Explainable AI , BERT , NLP

The Purpose

The BERT model has garnered immense popularity and has become the default choice for solving a wide range of NLP problems such as sentiment classification, question-answering, paraphrasing etc. It has demonstrated an exemplary performance on multiple NLP tasks that is significantly superior to any of its predecessor models. Nevertheless, it is critiqued for being a black-box with a very little understanding of how it works. BERT is also a transformer-based model and there are multiple components inside the model, with two of the major ones depicted below (If you are new to BERT, consider reading this amazing blog to understand the end-to-end architecture of transformer-based models). For the sake of understanding this blog, it is sufficient to abstract the understanding to this: (i) BERT consists of multiple internal components of which “Self-Attention” is quite central. (ii) Self-Attention consists of multiple attention heads.

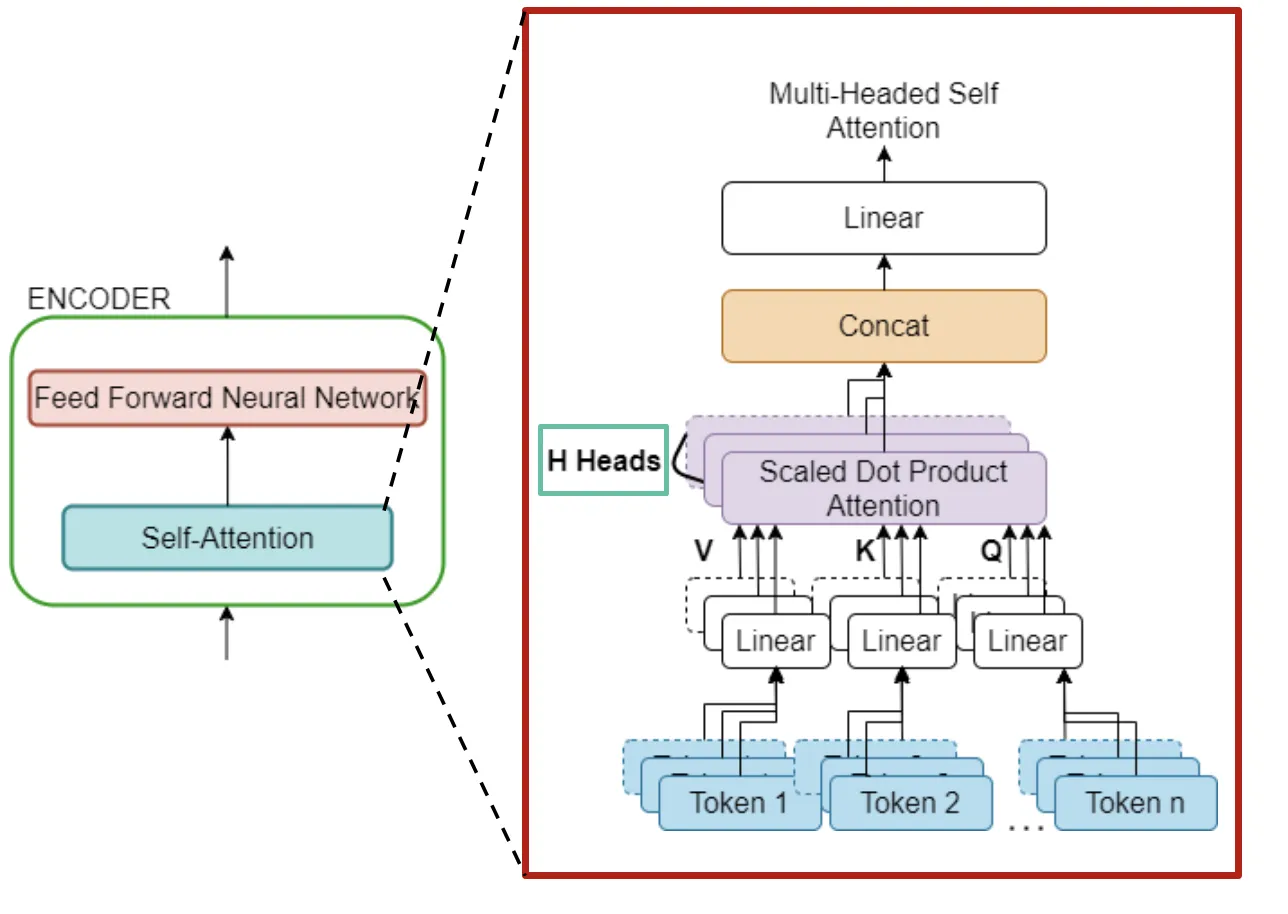
Self-Attention component consists of multiple attention heads

Since there are multiple attention heads, few questions such as “What does each attention head learn?” arise. Our work precisely tries to answer this question. We try to identify the various functional roles performed by different attention heads of BERT and how the behaviour changes when we do the fine-tuning.

What sets our work apart from the other contemporary approaches is the statistical rigour and formalism that our proposed methodology entails. Statistical testing is an integral part of research in many scientific fields. However, in the area of interpretability of NLP models, most works employ average-based measures or base their conclusions on a set of hand-picked sentences. Given the large variability that comes with each different input sentence, statistical testing is more than the need of the hour. Thus, the inferences we draw from our approach are robust and carefully arrived at.

The Approach

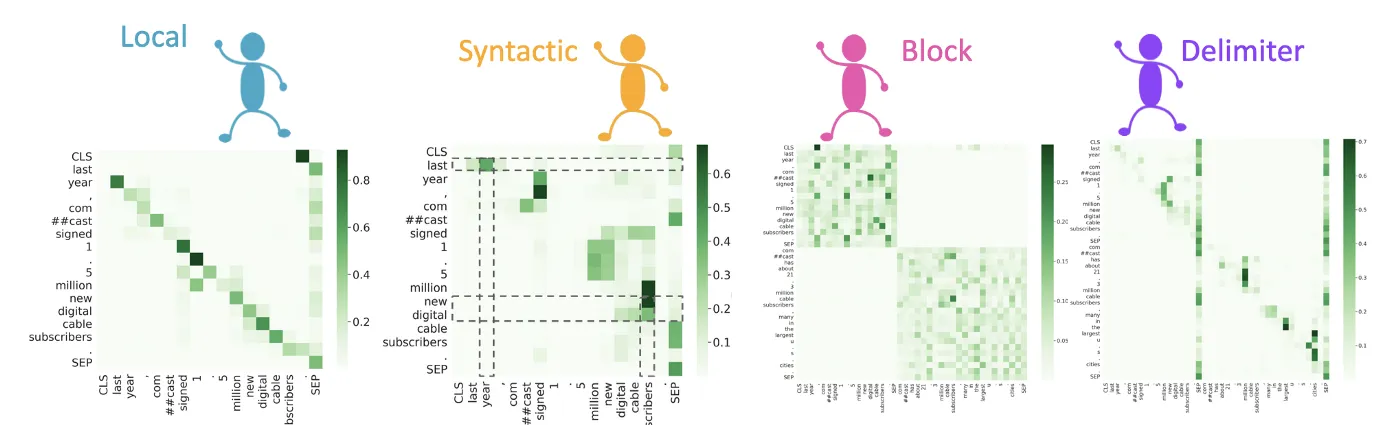
We consider 4 high-level functional roles: Local, Syntactic, Block and Delimiter. We propose a three step procedure for identifying the functional roles of heads:

(i) We first define a template for analysing attention patterns, we call it “Attention Sieves”.

(ii) We compute the metric of “Sieve Bias Score” for all attention heads and for all functional roles across all the input sequences.

(iii) We apply Hypothesis Testing to finally assign functional roles to the heads.

Attention Sieves

The set of tokens for a given functional role is defined as the attention sieve for a current token. The following figure would make it clearer.

Various attention sieves defined for functional roles. The lines are pointing to the words in the given attention sieve for the word in the box.

Sieve Bias Score

Across a sample of input sequences, we compute this metric for all functional roles and for all attention heads.

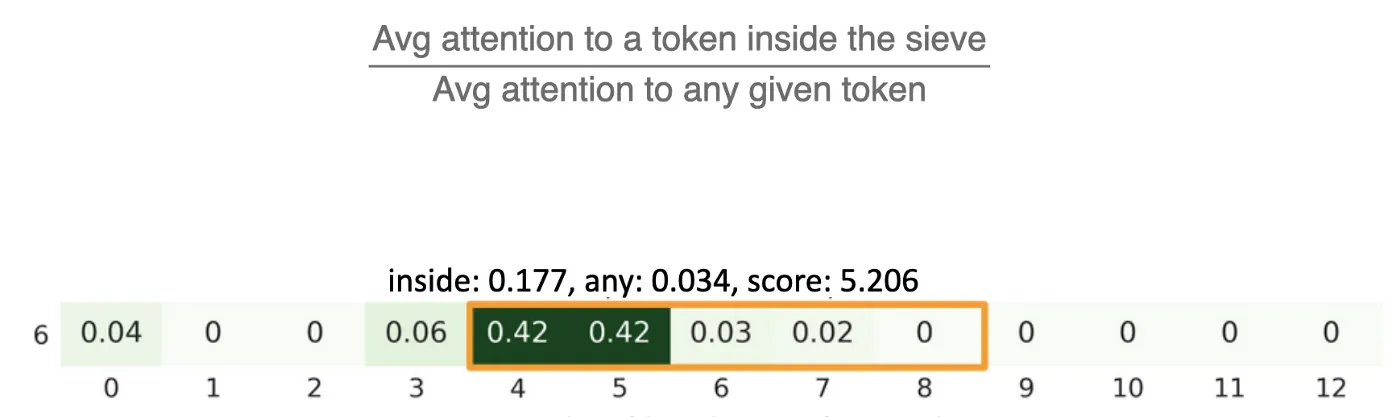
This indicates 5x more (than uniform) attention is given to the tokens inside this local attention sieve in this example

This metric quantifies the relative preference given to the tokens inside the attention sieve as opposed to the other tokens. Thus, we have a sieve bias score for each functional role, for each attention head, across a large sample of input sequences.

Hypothesis Testing

We need to aggregate the sieve bias scores across the input sequences. How do we do that? Simplest method involves taking average over the input sequences, so that we have a “single number” for each attention head and for each functional role. If the “single number” is high enough, then we say that this attention head can be assigned that functional role. However, such average-based measure is error prone, as the distribution of sieve bias score is not symmetric. We need something more accurate: Hypothesis Testing.

The Alternate Hypothesis: Mean of the sieve bias score across all input sequences is greater than or equal to some threshold τ.

The Null Hypothesis: Mean of the sieve bias score across all input sequences is less than to some threshold τ.

Null Hypothesis is setup for each attention head and for each functional role. We assign a given functional role f to an attention head only if the attention head rejects the Null Hypothesis setup for f. The following diagram pictorially depicts the functional role assignment strategy.

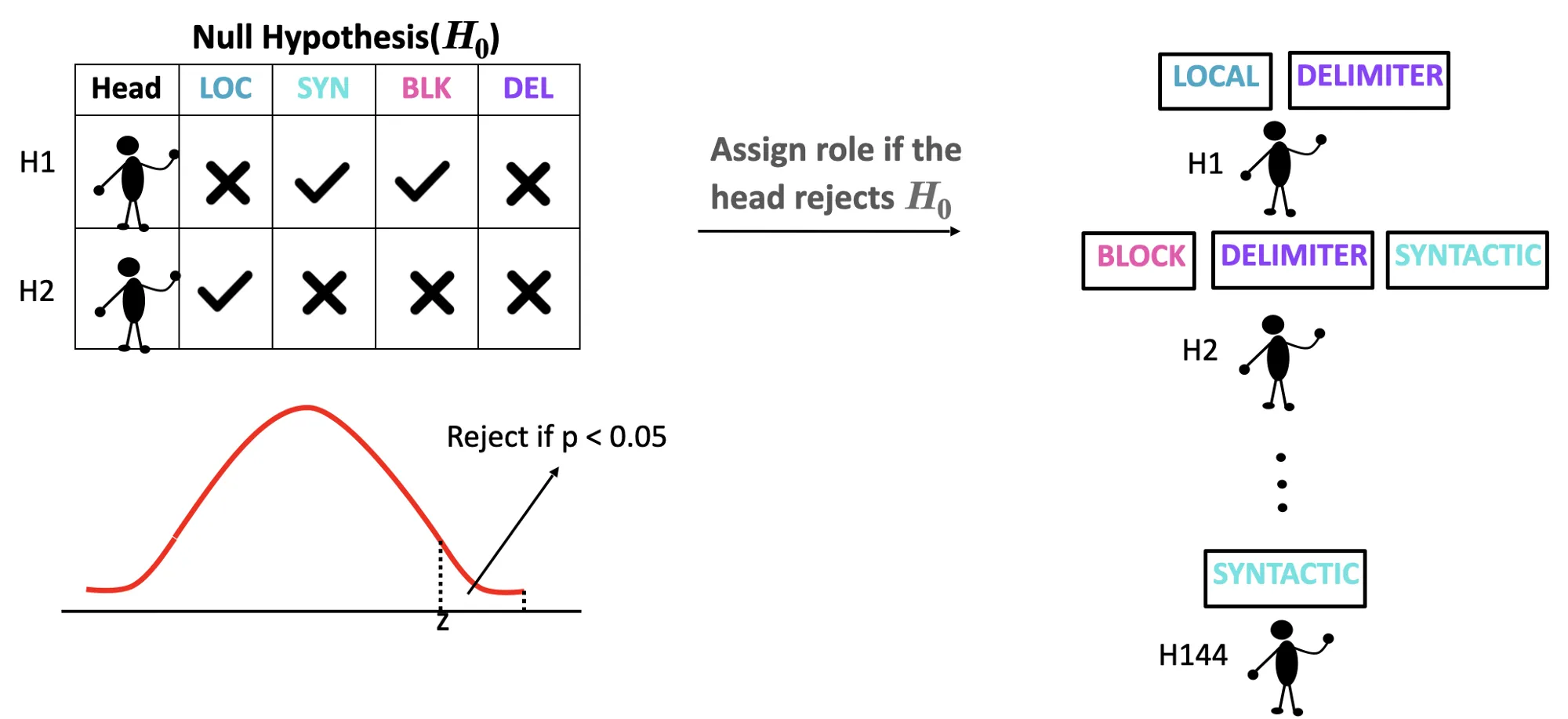
Functional Role Assignment: The ❌ in the table indicates rejection of Null Hypothesis whereas ✔ indicates acceptance of the same.

Using this process, we assign functional roles to all the attention heads of BERT. Next, we discuss the results and insights that draw from the assignment.

Results and Discussion

We discuss the results and answer three major research questions: (i) Are functional roles mutually exclusive? (ii) How are functional roles distributed across layers? (ii) What is the effect of fine-tuning on the functional roles?

Experimental Setup

We test our approach on four NLU tasks from the standard GLUE dataset. The tasks being Paraphrasing (MRPC and QQP), Sentiment Classification (SST-2), Natural Language Inferencing (QNLI).

1. Are functional roles mutually exclusive?

No, they are not. A single attention head can perform multiple functional roles, for example, it can be local as well as syntactic. The following diagram shows the sets of heads (represented by circle)and the overlap indicates the degree of multi-functionality.

  • There are a significant number of Delimiter Heads (73% across 4 GLUE tasks)
  • Overlap between Local and Syntactic heads is very high, ~ 42% to 89% across all tasks.

2. How are functional roles distributed across layers?

We split the 4 coarse functional roles (Local, Syntactic, Block, and Delimiter) into fine-grained roles.

Syntactic Role is further studies as nsubj, dobj, amod, advmod

Delimiter Role is is separately studied for CLS and SEP token.

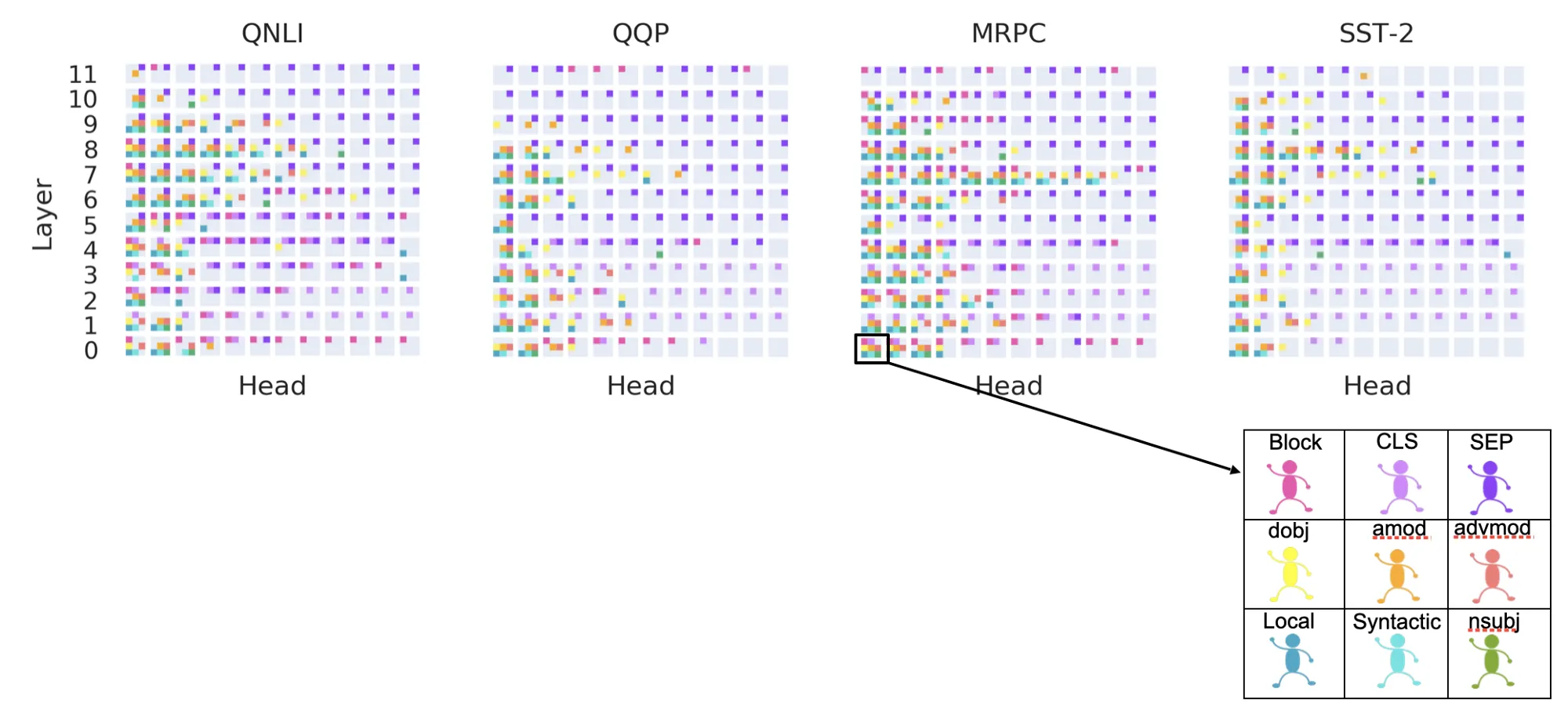
Functional Roles assigned to all the attention heads. The colours indicate the respective functional roles.

  • The number of multi-functional heads is higher in the middle layers (layers 5 to 9) for MRPC, QNLI and SST-2. However for QQP, these heads are more in the initial layers.
  • Delimiter heads (attending to SEP) are in the later layers.
  • Heads attending to the CLS token are in the initial layers.
  • Block heads are mostly present in the zero-th layer. Their presence in the later layers varies from one task to another.
  • There are at least 3 syntactic heads in each layer (except a very few exceptions).
  • Lastly, across the four tasks, there are very few multi-functional heads in the last two layers.

3. What is the effect of fine-tuning on the functional roles?

BERT undergoes a two-phase training process; first is the pre-training phase and second is the task-specific fine-tuning. In this section, we study how these functional roles change when we fine-tune the BERT model. We observe that the functional roles get distributed in the later layers during the fine-tuning.

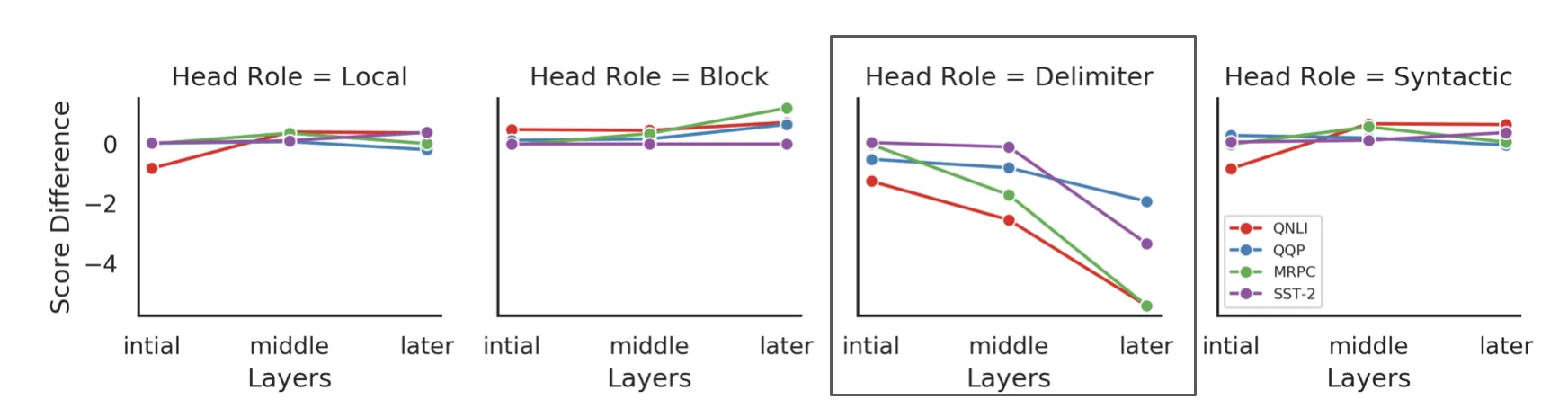
Changes in the functional behaviour as part of fine-tuning.

  • As part of fine-tuning, there is a decrease in the attention on SEP token, that is distributed to other tokens of the input sequence.
  • Reinforces the hypothesis made in Clark et al. that [SEP] tokens are no-op indicator, so attentive bias to those tokens is reducing as fine-tuning specializes the final layers.

Summary

This work presents a statistical technique to identify the roles played by attention heads of BERT, wherein all different functional roles can be analyzed with the same unified approach. This helps to shed light on how attention heads work and encourage the design of interpretable models.

For more details and nuances, please consider reading our full paper: here